Based on new research, the article presents a formula for determining the potential energy of an earthquake with incorporation of seismic moment and displacement angle values. This formula is new compared to the one derived by the author earlier. The mechanical interpretation of the new formula is provided. Much effort is devoted to determining the values of “stress relief” during strong earthquakes. A formula is derived for determining the values of “stress relief” based on shear modulus and ultimate shear strain of the soil stratum at the epicenters of 44 earthquakes. Also, a methodology is offered to determine energy values of earthquakes with complex structures of surface rupture, as well as areas of deformation zones on Earth’s surface and areas of strong earthquake aftershocks’ locations. New formulas are derived for determining such areas and a comparative analysis is provided with similar formulas by K. Kasahara and T. Dambara.
| Published in | Earth Sciences (Volume 14, Issue 1) |
| DOI | 10.11648/j.earth.20251401.13 |
| Page(s) | 33-48 |
| Creative Commons |
This is an Open Access article, distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution and reproduction in any medium or format, provided the original work is properly cited. |
| Copyright |
Copyright © The Author(s), 2025. Published by Science Publishing Group |
Earthquake Energy, Seismic Moment, Displacement Angle, Stress Relief, Deformation Areas and Aftershock Locations, Empirical Dependencies
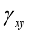 ,
, 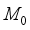 on the entire space of the deformed medium, on both sides of the future rupture caused by the pending earthquake.
on the entire space of the deformed medium, on both sides of the future rupture caused by the pending earthquake. 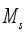 . In parallel, formula (3) can be used to determine the ultimate shear strain and tangential stresses for any points of the deformed medium
. In parallel, formula (3) can be used to determine the ultimate shear strain and tangential stresses for any points of the deformed medium 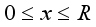 , based on the following formulas:
, based on the following formulas: 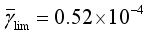 . It is shown in
. It is shown in 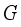 of the rocks in the Earth’s crust. In seismology and geotechnology, for the upper, near-surface rocks value is accepted as kg/cm2. Assuming that kg/cm2, the last column of Table 1 shows the stress relief values for 44 earthquakes, which are in the range from 2 to 57.5 kg/cm2. The stronger the earthquake, the higher the stress relief values.
of the rocks in the Earth’s crust. In seismology and geotechnology, for the upper, near-surface rocks value is accepted as kg/cm2. Assuming that kg/cm2, the last column of Table 1 shows the stress relief values for 44 earthquakes, which are in the range from 2 to 57.5 kg/cm2. The stronger the earthquake, the higher the stress relief values. 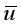 . Our research shows that for the 44 selected earthquakes, mean slip values
. Our research shows that for the 44 selected earthquakes, mean slip values 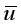 are 1.95-2.08 times smaller than the maximum slip values (Figure 5).
are 1.95-2.08 times smaller than the maximum slip values (Figure 5). No. | Country | Earthquake location | Date of earthquake occurrence | Type of slip | Earthquake magnitude | Rupture length , [km] | Rupture depth , [km] | Maximum slip , [m] |
|---|---|---|---|---|---|---|---|---|
1 | USA | Fort Tejon | 09.01.1857 | RL | 8.3 | 297 | 12 | 9.4 |
2 | USA | Owens Valley | 26.03.1872 | RL-N | 8 | 108 | 15 | 11 |
3 | Japan | Nobi | 27.10.1891 | LL | 8 | 80 | 15 | 8 |
4 | Japan | Rikuu | 31.08.1896 | R | 7.2 | 40 | 21 | 4.4 |
5 | USA | San Francisco | 1/13/1906 | RL | 7.8 | 432 | 12 | 6.1 |
6 | USA | Pleasant Valley | 10/3/1915 | N | 7.6 | 62 | 15 | 5.8 |
7 | China | Kansy | 12/16/1920 | LL | 8.5 | 220 | 20 | 10 |
8 | Japan | North Izu | 11/25/1930 | LL- R | 7.3 | 35 | 12 | 3.8 |
9 | China | Kehetuohai | 8/10/1931 | RL | 7.9 | 180 | 20 | 14.6 |
10 | Turkey | Erzincan | 12/26/1939 | RL | 7.8 | 360 | 20 | 7.5 |
11 | USA | Imperial Valley | 5/19/1940 | RL | 7.2 | 60 | 11 | 5.9 |
12 | China | Damxung | 11/18/1951 | RL | 8 | 200 | 10 | 12 |
13 | USA | Dixie Valley | 12/16/1954 | RL-R | 6.8 | 45 | 14 | 3.8 |
14 | Turkey | Abant | 5/26/1957 | RL | 7 | 40 | 8 | 1.65 |
15 | Mongolia | Gobi-Altai | 12/4/1957 | LL | 7.9 | 300 | 20 | 9.6 |
16 | USA | Hebgen Lake | 8/18/1959 | N | 7.6 | 45 | 17 | 6.1 |
17 | Iran | Dasht-e-Bayaz | 8/31/1968 | LL | 7.1 | 110 | 20 | 5.2 |
18 | Turkey | Gediz | 3/28/1970 | N | 7.1 | 63 | 17 | 2.8 |
19 | USA | San Fernando | 2/9/1971 | R-LL | 6.5 | 17 | 14 | 2.5 |
20 | China | Luhuo | 2/6/1973 | LL | 7.3 | 110 | 13 | 3.6 |
21 | Guatemala | Motagua | 2/4/1976 | LL | 7.5 | 257 | 13 | 3.4 |
22 | Turkey | Caldiran | 11/24/1976 | RL | 7.3 | 90 | 18 | 3.5 |
23 | Iran | Bob-Tangol | 12/19/1977 | RL | 5.8 | 14 | 12 | 0.3 |
24 | Greece | Thessaloniki | 6/20/1978 | N | 6.4 | 28 | 14 | 0.22 |
25 | Iran | Tabas-e-Colshan | 9/16/1978 | R | 7.5 | 74 | 22 | 3 |
26 | USA | Homestead Valley | 3/15/1979 | RL | 5.6 | 6 | 4 | 0.1 |
27 | Australia | Cadoux | 6/2/1979 | R | 6.1 | 16 | 6 | 1.5 |
28 | USA | El Centro | 10/15/1979 | RL | 6.7 | 51 | 12 | 0.8 |
29 | Iran | Koli | 11/27/1979 | LL-R | 7.1 | 75 | 22 | 3.9 |
30 | Algeria | El Asman | 10/10/1980 | R | 7.3 | 55 | 15 | 6.5 |
31 | Italy | South Apennines | 11/23/1980 | N | 6.9 | 60 | 15 | 1.15 |
32 | Greece | Corinth | 2/25/1981 | N | 6.4 | 19 | 16 | 1.5 |
33 | Greece | Corinth | 3/4/1981 | N | 6.4 | 26 | 18 | 1.1 |
34 | USA | Borah Peak | 10/28/1983 | N-LL | 7.3 | 33 | 20 | 2.7 |
35 | Algeria | Constantine | 10/27/1985 | LL | 5.9 | 21 | 13 | 0.12 |
36 | Australia | Marryat Creek | 3/30/1986 | R-LL | 5.8 | 13 | 3 | 1.3 |
37 | Greece | Kalamata | 9/13/1986 | N | 5.8 | 15 | 14 | 0.18 |
38 | New Zealand | Edgecumbe | 3/2/1987 | N | 6.6 | 32 | 14 | 2.9 |
39 | USA | Superstition Hills | 11/24/1987 | RL | 6.6 | 30 | 11 | 0.92 |
40 | Australia | Tennant Greek | 1/22/1988 | R | 6.3 | 13 | 9 | 1.3 |
41 | China | Lancand Gengma | 11/6/1988 | RL | 7.3 | 80 | 20 | 1.5 |
42 | Armenia | Spitak | 12/7/1988 | R-RL | 6.8 | 38 | 11 | 2 |
43 | Canada | Ungava | 12/25/1989 | R | 6.3 | 10 | 5 | 2 |
44 | USA | Landers | 6/28/1992 | RL | 7.6 | 62 | 12 | 6 |
No. | Mean slip , [m] | Seismic moment , [dyne*cm] | Value of from (2), [km] | Energy classes (1) | Energy classes (8) | Ultimate shear strain from (12) | Stress relief , kg/cm2 kg/cm2 |
|---|---|---|---|---|---|---|---|
1 | 6.4 | 114.0 | 47 | 16.68 | 16.79 | 1.07 | 53.5 |
2 | 6 | 48.60 | 45 | 16.30 | 16.41 | 1.05 | 52.5 |
3 | 5.04 | 30.24 | 40.25 | 16.06 | 16.17 | 0.98 | 49 |
4 | 2.59 | 10.88 | 27.95 | 15.49 | 15.60 | 0.73 | 36.5 |
5 | 3.3 | 85.54 | 31.5 | 16.44 | 16.54 | 0.82 | 41 |
6 | 2 | 9.300 | 25 | 15.36 | 15.47 | 0.63 | 31.5 |
7 | 7.25 | 159.5 | 51.25 | 16.84 | 16.95 | 1.11 | 55.5 |
8 | 2.9 | 6.090 | 29.5 | 15.26 | 15.37 | 0.77 | 38.5 |
9 | 7.38 | 132.8 | 51.9 | 16.76 | 16.87 | 1.12 | 56 |
10 | 1.85 | 66.60 | 24.25 | 16.19 | 16.30 | 0.60 | 30 |
11 | 1.5 | 4.950 | 22.5 | 15.01 | 15.11 | 0.52 | 26 |
12 | 8 | 80.00 | 65 | 16.55 | 16.66 | 1.15 | 57.5 |
13 | 2.1 | 6.615 | 25.5 | 15.22 | 15.33 | 0.65 | 32.5 |
14 | 0.55 | 0.880 | 17.75 | 13.92 | 14.02 | 0.24 | 12 |
15 | 6.54 | 196.2 | 47.7 | 16.92 | 17.03 | 1.08 | 54 |
16 | 2.14 | 8.186 | 25.7 | 15.32 | 15.42 | 0.65 | 32.5 |
17 | 2.3 | 25.30 | 26.5 | 15.83 | 15.93 | 0.68 | 34 |
18 | 0.86 | 4.605 | 19.3 | 14.80 | 14.91 | 0.35 | 17.5 |
19 | 1.5 | 1.785 | 22.5 | 14.56 | 14.67 | 0.52 | 26 |
20 | 1.3 | 9.295 | 21.5 | 15.24 | 15.34 | 0.47 | 23.5 |
21 | 2.6 | 43.43 | 28 | 16.09 | 16.20 | 0.73 | 36.5 |
22 | 2.05 | 16.61 | 25.25 | 15.62 | 15.73 | 0.64 | 32 |
23 | 0.12 | 0.101 | 15.6 | 12.38 | 12.48 | 0.06 | 3 |
24 | 0.08 | 0.157 | 15.4 | 12.40 | 12.50 | 0.04 | 2 |
25 | 1.5 | 12.21 | 22.5 | 15.39 | 15.50 | 0.52 | 26 |
26 | 0.05 | 0.006 | 15.25 | 10.78 | 10.95 | 0.03 | 1.5 |
27 | 0.5 | 0.240 | 17.5 | 13.32 | 13.42 | 0.22 | 11 |
28 | 0.18 | 0.551 | 15.9 | 13.28 | 13.39 | 0.09 | 4.5 |
29 | 1.2 | 9.900 | 21 | 15.24 | 15.35 | 0.45 | 22.5 |
30 | 1.54 | 6.353 | 22.7 | 15.12 | 15.23 | 0.53 | 26.5 |
31 | 0.64 | 2.880 | 18.2 | 14.49 | 14.61 | 0.28 | 14 |
32 | 0.6 | 0.912 | 18 | 13.97 | 14.07 | 0.26 | 13 |
33 | 0.6 | 1.404 | 18 | 14.16 | 14.26 | 0.26 | 13 |
34 | 0.8 | 2.640 | 19 | 14.53 | 14.64 | 0.33 | 16.5 |
35 | 0.1 | 0.137 | 15.5 | 12.43 | 12.53 | 0.05 | 2.5 |
36 | 0.5 | 0.098 | 17.5 | 12.93 | 13.03 | 0.22 | 11 |
37 | 0.15 | 0.158 | 15.75 | 12.66 | 12.74 | 0.07 | 3.5 |
38 | 1.7 | 3.808 | 23.5 | 14.93 | 15.04 | 0.57 | 28.5 |
39 | 0.54 | 0.891 | 17.5 | 13.92 | 14.03 | 0.24 | 12 |
40 | 0.63 | 0.369 | 18.15 | 13.59 | 13.70 | 0.27 | 13.5 |
41 | 0.7 | 5.600 | 18.5 | 14.81 | 14.92 | 0.30 | 15 |
42 | 1.22 | 2.550 | 21.1 | 14.65 | 14.76 | 0.45 | 22.5 |
43 | 0.8 | 0.200 | 19 | 13.41 | 13.52 | 0.33 | 16.5 |
44 | 2.95 | 10.97 | 29.75 | 15.52 | 15.63 | 0.78 | 39 |
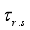 on rupture middle areas will be about twice as high, so will reach from 4 to 115 kg/cm2. According to Brune
on rupture middle areas will be about twice as high, so will reach from 4 to 115 kg/cm2. According to Brune 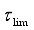 usually are in the range of 50-100 bar (kg/cm2), with some as low as a few bars and some others as high as a few hundredbars. For the San Francisco earthquake of 1906 (), the stress relief value was estimated by geodetic methods to be 130 bars.
usually are in the range of 50-100 bar (kg/cm2), with some as low as a few bars and some others as high as a few hundredbars. For the San Francisco earthquake of 1906 (), the stress relief value was estimated by geodetic methods to be 130 bars. 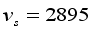 m/sec), based on synthetic accelerograms of earthquakes with magnitudes of 7.0, 8.0 and 9.0, at the bedding’s base level (depth of 30 m) the design values of
m/sec), based on synthetic accelerograms of earthquakes with magnitudes of 7.0, 8.0 and 9.0, at the bedding’s base level (depth of 30 m) the design values of 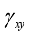 reach
reach 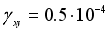 ,
, 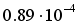 and
and  , respectively, while the stress relief values at kg/cm2 reach 25 kg/cm2 at , 44 kg/cm2 at , and 64 kg/cm2 at .
, respectively, while the stress relief values at kg/cm2 reach 25 kg/cm2 at , 44 kg/cm2 at , and 64 kg/cm2 at . 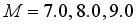 , respectively.
, respectively. 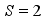 m (measured on-site after the earthquake), vertical component - m, compression component - m, horizontal component m, R=1090, P=530.
m (measured on-site after the earthquake), vertical component - m, compression component - m, horizontal component m, R=1090, P=530. No. earthquake | Country | Earthquake location | Date of the earthquake | Earthquake Magnitude | Length of the gap (km) | Depth of the rupture h (km) | Maximum movement (m) | Average movement (m) |
|---|---|---|---|---|---|---|---|---|
1 | USA | Fort Tejon | 09.01.1857 | 8.3 | 297 | 12 | 9.4 | 6.4 |
2 | USA | Owens Valley | 26.03.1872 | 8 | 108 | 15 | 11 | 6 |
3 | Japan | Nobi | 27.10.1891 | 8 | 80 | 15 | 8 | 5.04 |
4 | Japan | Rikuu | 31.08.1896 | 7.2 | 40 | 21 | 4.4 | 2.59 |
5 | USA | San Francisco | 1/13/1906 | 7.8 | 432 | 12 | 6.1 | 3.3 |
6 | USA | Pleasant Valley | 10/3/1915 | 7.6 | 62 | 15 | 5.8 | 2 |
7 | China | Kansy | 12/16/1920 | 8.5 | 220 | 20 | 10 | 7.25 |
8 | Japan | North Izu | 11/25/1930 | 7.3 | 35 | 12 | 3.8 | 2.9 |
9 | China | Kehetuohai | 8/10/1931 | 7.9 | 180 | 20 | 14.6 | 7.38 |
10 | Turkеy | Erzihcan | 12/26/1939 | 7.8 | 360 | 20 | 7.5 | 1.85 |
11 | USA | Imperial Valley | 5/19/1940 | 7.2 | 60 | 11 | 5.9 | 1.5 |
12 | China | Damxung | 11/18/1951 | 8 | 200 | 10 | 12 | 8 |
13 | Turkеy | Abant | 5/26/1957 | 7 | 40 | 8 | 1.65 | 0.55 |
14 | Mongolia | Gobi-Altai | 12/4/1957 | 7.9 | 300 | 20 | 9.6 | 6.54 |
15 | USA | Hebgen Lake | 8/18/1959 | 7.6 | 45 | 17 | 6.1 | 2.14 |
16 | Iran | Dasht-e-Bayaz | 8/31/1968 | 7.1 | 110 | 20 | 5.2 | 2.3 |
17 | Turkеy | Gediz | 3/28/1970 | 7.1 | 63 | 17 | 2.8 | 0.86 |
18 | China | Luhuo | 2/6/1973 | 7.3 | 110 | 13 | 3.6 | 1.3 |
19 | Guatemala | Motagua | 2/4/1976 | 7.5 | 257 | 13 | 3.4 | 2.6 |
20 | Turkеy | Caldiran | 11/24/1976 | 7.3 | 90 | 18 | 3.5 | 2.05 |
21 | Iran | Tabas-e-Colshan | 9/16/1978 | 7.5 | 74 | 22 | 3 | 1.5 |
22 | Iran | Koli | 11/27/1979 | 7.1 | 75 | 22 | 3.9 | 1.2 |
23 | Algeria | El Asman | 10/10/1980 | 7.3 | 55 | 15 | 6.5 | 1.54 |
24 | USA | Borah Peak | 10/28/1983 | 7.3 | 33 | 20 | 2.7 | 0.8 |
25 | Armenia | Spitak | 12/7/1988 | 7 | 38 | 11 | 2 | 1.22 |
26 | China | Lancand Gengma | 11/6/1988 | 7.3 | 80 | 20 | 1.5 | 0.7 |
27 | USA | Landers | 6/28/1992 | 7.6 | 62 | 12 | 6 | 2.95 |
No. earthquake | The value of according to the formula (2) (km) | Size of the area Q1/1014, to the formula (15), cm2 | Size of the area Q2/1014, to the formula (16), cm2 | Difference in areas Q1-Q2=<i></i>Q/1014, cm2 | Deviations <i></i>Q/Q2 in % | Deviations Q1/Q2 |
|---|---|---|---|---|---|---|
1 | 47 | 3.02 | 2.92 | 0.10 | 3.42 | 1.03 |
2 | 45 | 0.97 | 1.45 | -0.48 | -33.10 | 0.67 |
3 | 40.25 | 0.64 | 1.45 | -0.81 | -55.86 | 0.44 |
4 | 27.95 | 0.22 | 0.22 | 0.00 | 0.00 | 1.00 |
5 | 31.5 | 2.72 | 0.90 | 1.82 | 202 | 3.02 |
6 | 25 | 0.31 | 0.56 | -0.25 | -44.64 | 0.55 |
7 | 51.25 | 2.26 | 4.68 | -2.42 | -51.71 | 0.48 |
8 | 29.5 | 0.21 | 0.28 | -0.07 | -25.00 | 0.75 |
9 | 51.9 | 1.87 | 1.14 | 0.73 | 64.04 | 1.64 |
10 | 24.25 | 1.75 | 0.90 | 0.85 | 94.44 | 1.94 |
11 | 22.5 | 0.27 | 0.22 | 0.05 | 22.73 | 1.23 |
12 | 65 | 2.60 | 1.45 | 1.15 | 79.31 | 1.79 |
13 | 17.75 | 0.14 | 0.14 | 0.00 | 0.00 | 1.00 |
14 | 47.7 | 2.86 | 1.14 | 1.72 | 151 | 2.51 |
15 | 25.7 | 0.23 | 0.56 | -0.33 | -58.93 | 0.41 |
16 | 26.5 | 0.58 | 0.17 | 0.41 | 241 | 3.41 |
17 | 19.3 | 0.24 | 0.17 | 0.07 | 41.18 | 1.41 |
18 | 21.5 | 0.47 | 0.28 | 0.19 | 67.86 | 1.68 |
19 | 28 | 1.44 | 0.45 | 0.99 | 220 | 3.20 |
20 | 25.25 | 0.45 | 0.28 | 0.17 | 60.71 | 1.61 |
21 | 22.5 | 0.33 | 0.45 | -0.12 | -26.67 | 0.73 |
22 | 21 | 0.32 | 0.17 | 0.15 | 88.24 | 1.88 |
23 | 22.7 | 0.25 | 0.28 | -0.03 | -10.71 | 0.89 |
24 | 19 | 0.13 | 0.28 | -0.15 | -54 | 0.46 |
25 | 21.1 | 0.16 | 0.14 | 0.02 | 14.29 | 1.14 |
26 | 18.5 | 0.30 | 0.28 | 0.02 | 7.14 | 1.07 |
27 | 29.75 | 0.37 | 0.56 | -0.19 | -33.93 | 0.66 |
Average value Average value without earthquakes № 5, 14, 16, 19 | 36 | 1.36 | ||||
6.49 | 1.06 | |||||
| [1] | Khachiyan E. Y., Method for determining the potential strain energy stored in the earth before a large earthquake. Science Publishing Group, Earth Sciences, 2013, 10(2), pp. 47-57., |
| [2] | Khachiyan E. Y., On determining of the ultimate strain of earth crust rocks by the value of relative slips on the earth surface after a large earthquake. Science Publishing Group, Earth Sciences, 2016, 5, pp. 111-118, |
| [3] | Khachiyan E. Y., Predicting of the seismogram and accelerogram of strong motions of the soil for an earthquake model considered as an instantaneous rupture of the earth’s surface. Science Publishing Group, Earth Sciences, 2018, 7, pp. 183-201. |
| [4] | Khachiyan E. Y., Analysis of the Values of Ground Displacements, Shear Strains, Velocities and Accelerations, and Response Spectra of Strong Earthquake by Synthetic Accelerograms. Science Publishing Group, Earth Sciences, 2022, 11(5), pp. 327-337, |
| [5] | Brune J. N., Seismic Risk and Engineering Decisions, The Physics of Earthquake Strong Motion, in Lomnitz C. and Rosenblueth E., Eds., New York: Elsevier Sci. Publ. Co., 1976, pp. 141-177. |
| [6] | Aki K. Generation and propagation of G waives from the Niigata Earthquake of June, 16, 1964, Estimation of Earthquake moment, Released energy, and stress –strain drop from G wave spectrum. Bull. Earthquake Res. Inst., Tokyo Univ., 1966, 44: 73-88. |
| [7] | Timoshenko S., Gere J. Mechanics of Materials, New York, Nan Nostrand Renhold Company, 1972, P. 669. |
| [8] | Wells D. L., and Coppersmith K. I., New Empirical Rela¬tionship among Magnitude, Rupture Length, Rupture Width, Rupture Area, and Surface Displacement, Bull. Seismol. Soc. Amer., 1994, vol. 84, no. 4, pp. 974-1002. |
| [9] | Cisternas A., Philip H., Bousquet J. C., Cara M., Deschamps A., Dorbath L., Dorbath C., Haessler H., Jimenez E., Nercessian A., Rivera L., Romanowicz B., Gvishiani A., Shebalin N. V., Aptekman I., Arefiev S., Borisov B. A., Gorshkov A., Graizer V., Lander A., Pletnev K., Rogozhin A. I., Tatevossian R. The Spitak (Armenia) earthquake of 7 December 1988: field observations, seismology and tectonics // Nature. 1989. V. 339. P. 675–679. |
| [10] | Kasahara K. Earthquake Mechanics, Cambridge University Press, 1981, P. 263. |
| [11] | Dambara T. A revised relation between the area of the crustal deformation associated with an earthquake and its magnitude // Rep. Coord. Comm. Earthq. Predict. 1979. V. 21. P. 167–169. [in Japanese]. |
| [12] | Mogi K. Earthquake Prediction, Academic Press, 1985, P. 382. |
| [13] | Rikitake T. Earthquake Prediction. Elsevier Scientific Publishing. Amsterdam, 1976, P. 357. |
| [14] | Khachiyan E. Y. On a Simple Method for Determining the Potential Strain Energy Stored in the Earth before a Large Earthquake. Journal of Volcanology and Seismology, 2011, Vol. 5, No. 4, pp. 286-297. Pleiades Publishing, Ltd., 2011, |
| [15] | Sharp R. V. Surface Faulting: A preliminary view. Earthquake Spectra. The Professional Journal of the Earthquake Engineering Institute, USA, Special Supplement, Armenia Earthquake Reconnaissance Report, August 1989, pp. 13-22. |
APA Style
Khachiyan, E. (2025). On the Relationships Between the Main Parameters of an Earthquake and Its Actual Consequences on the Earth's Surface the Magnitude and Seismic Moment of Earthquake. Earth Sciences, 14(1), 33-48. https://doi.org/10.11648/j.earth.20251401.13
ACS Style
Khachiyan, E. On the Relationships Between the Main Parameters of an Earthquake and Its Actual Consequences on the Earth's Surface the Magnitude and Seismic Moment of Earthquake. Earth Sci. 2025, 14(1), 33-48. doi: 10.11648/j.earth.20251401.13
AMA Style
Khachiyan E. On the Relationships Between the Main Parameters of an Earthquake and Its Actual Consequences on the Earth's Surface the Magnitude and Seismic Moment of Earthquake. Earth Sci. 2025;14(1):33-48. doi: 10.11648/j.earth.20251401.13
@article{10.11648/j.earth.20251401.13,
author = {Eduard Khachiyan},
title = {On the Relationships Between the Main Parameters of an Earthquake and Its Actual Consequences on the Earth's Surface the Magnitude and Seismic Moment of Earthquake},
journal = {Earth Sciences},
volume = {14},
number = {1},
pages = {33-48},
doi = {10.11648/j.earth.20251401.13},
url = {https://doi.org/10.11648/j.earth.20251401.13},
eprint = {https://article.sciencepublishinggroup.com/pdf/10.11648.j.earth.20251401.13},
abstract = {Based on new research, the article presents a formula for determining the potential energy of an earthquake with incorporation of seismic moment and displacement angle values. This formula is new compared to the one derived by the author earlier. The mechanical interpretation of the new formula is provided. Much effort is devoted to determining the values of “stress relief” during strong earthquakes. A formula is derived for determining the values of “stress relief” based on shear modulus and ultimate shear strain of the soil stratum at the epicenters of 44 earthquakes. Also, a methodology is offered to determine energy values of earthquakes with complex structures of surface rupture, as well as areas of deformation zones on Earth’s surface and areas of strong earthquake aftershocks’ locations. New formulas are derived for determining such areas and a comparative analysis is provided with similar formulas by K. Kasahara and T. Dambara.},
year = {2025}
}
TY - JOUR T1 - On the Relationships Between the Main Parameters of an Earthquake and Its Actual Consequences on the Earth's Surface the Magnitude and Seismic Moment of Earthquake AU - Eduard Khachiyan Y1 - 2025/02/26 PY - 2025 N1 - https://doi.org/10.11648/j.earth.20251401.13 DO - 10.11648/j.earth.20251401.13 T2 - Earth Sciences JF - Earth Sciences JO - Earth Sciences SP - 33 EP - 48 PB - Science Publishing Group SN - 2328-5982 UR - https://doi.org/10.11648/j.earth.20251401.13 AB - Based on new research, the article presents a formula for determining the potential energy of an earthquake with incorporation of seismic moment and displacement angle values. This formula is new compared to the one derived by the author earlier. The mechanical interpretation of the new formula is provided. Much effort is devoted to determining the values of “stress relief” during strong earthquakes. A formula is derived for determining the values of “stress relief” based on shear modulus and ultimate shear strain of the soil stratum at the epicenters of 44 earthquakes. Also, a methodology is offered to determine energy values of earthquakes with complex structures of surface rupture, as well as areas of deformation zones on Earth’s surface and areas of strong earthquake aftershocks’ locations. New formulas are derived for determining such areas and a comparative analysis is provided with similar formulas by K. Kasahara and T. Dambara. VL - 14 IS - 1 ER -